

Blocks Demo. Flash Player 10 3D experiment. Revolver Maps - Free 3D Visitor Maps. Inside-out_torus_(animated,_small).gif (GIF Image, 170x170 pixels) Sphere-like_degenerate_torus.gif (GIF Image, 240x180 pixels) The HyperSphere. The mathematical objects that live on the sphere in four dimensional space -- the hypersphere -- are both beautiful and interesting.

The four dimensional sphere is a unique object, with properties both similar to and surprisingly different from those of our ordinary sphere. Similarly to the case in three dimensions, there is a family of Platonic and Archimedean solids that can be viewed on the four dimensional sphere. These shapes can be seen to have a structure that is comfortingly analogous to that of the Platonic solids we know and love. However, there are some properties of the four dimensional sphere that are startlingly different. In contrast to the ordinary sphere, it is possible to "comb the hair" on the four dimensional sphere. How do we view objects in four dimensions? First, what does it mean to look at an object that lives in four dimensional space? So what are we looking at? Suppose a flatlander wished to view structures on a sphere from his comfortable planar home. Flatland: The Movie - Official Trailer. Stereographic projection of Paris.jpg - Wikipedia, the free encyclopedia.
Polyhedron. A polyhedron is said to be convex if its surface (comprising its faces, edges and vertices) does not intersect itself and the line segment joining any two points of the polyhedron is contained in the interior or surface.
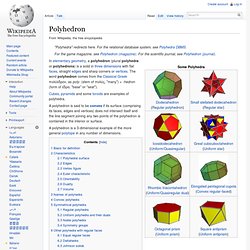
A polyhedron is a 3-dimensional example of the more general polytope in any number of dimensions. Basis for definition[edit] One modern approach treats a geometric polyhedron as a realisation of some abstract polyhedron. Any such polyhedron can be built up from different kinds of element or entity, each associated with a different number of dimensions: Different approaches - and definitions - may require different realisations. In such elementary and set-based definitions, a polyhedron is typically understood as a three-dimensional example of the more general polytope in any number of dimensions.
More generally in other mathematical disciplines, "polyhedron" is used to refer to a variety of related constructs, some geometric and others purely algebraic or abstract. . . . Uniform polychoron. In geometry, a uniform polychoron (plural: uniform polychora) is a polychoron (4-polytope) which is vertex-transitive and whose cells are uniform polyhedra.
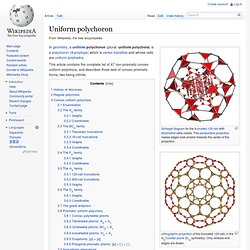
This article contains the complete list of 47 non-prismatic convex uniform polychora, and describes three sets of convex prismatic forms, two being infinite. History of discovery[edit] Regular polychora[edit] The uniform polychora include two special subsets, which satisfy additional requirements: 120-cell.gif - Wikipedia, the free encyclopedia. 120-cell-inner.gif (GIF Image, 256x256 pixels) 120-cell.gif (GIF Image, 256x256 pixels) 120 Cell. Install This program requires an OpenGL accelerated graphics card, and will require you to install the .Net framework.
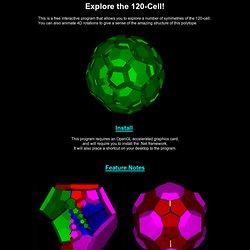
It will also place a shortcut on your desktop to the program. Feature Notes I have also seen the 120-cell referred to as the "dodecaplex". After seeing this program, my wife called me a dodecadork. 120 Cell Features. Here are some quick feature notes.

This is not the full list of features, more just a list of items that may not be directly obvious from UI. Mouse Dragging Dragging the mouse with the left button down will rotate the puzzle in 3D. Dragging the mouse with the right button down will zoom in and out. Graphics Archive - The Order-7 Borromean Ring Orbifold by Charlie Gunn (Science U) [ Graphics Archive | Up | Comments ]
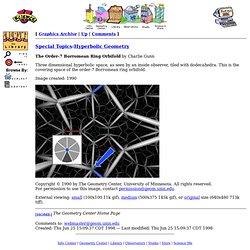
Graphics Archive - Special Topics:Hyperbolic Geometry (Science U) Graphics Archive - Escher Fish by Silvio Levy (Science U) Escher. LW434.jpg (JPEG Image, 425x425 pixels) Hyperbolic Tesselations Applet. Hyperbolic Tesselations Applet The following keys and mouse actions do interesting things: (NOTE: you may have to click on the applet once before it will accept keyboard input.
On some browsers (mozilla) you may have to leave and re-enter the browser window.) Soon to come: antialiasing resizable friendly gui instead of these lame key controls high-quality image or postscript dumps filled and colored faces For experts: You can also specify a general uniform tiling, using a simplified version of the Burgiel/Conway/Goodman-Strauss (BCGS) orbifold symbol, which will be explained below. POV-Ray: Download. Poincaré Hyperbolic Disk.
The Poincaré hyperbolic disk is a two-dimensional space having hyperbolic geometry defined as the disk , with hyperbolic metric The Poincaré disk is a model for hyperbolic geometry in which a line is represented as an arc of a circle whose ends are perpendicular to the disk's boundary (and diameters are also permitted).
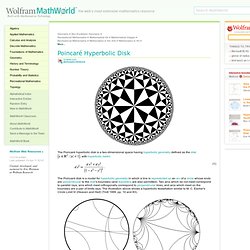
Two arcs which do not meet correspond to parallel rays, arcs which meet orthogonally correspond to perpendicular lines, and arcs which meet on the boundary are a pair of limits rays. The illustration above shows a hyperbolic tessellation similar to M. Math Artwork. This 3D vortex image is hidden in the above picture.

To see it, relax your eyes and focus behind the screen. This autostereogram was generated with William Steer’s free autostereogram generating program SISgen. Click here to see an animated version of this picture. I also have a Mathematica-only version of this picture, but it is not as accurate. See also Pascal Massimino’s “Maelstrom” autostereogram. Icophase.MOV (video/quicktime Object) Geotriacon.JPG (JPEG Image, 640x480 pixels) Gold_icosa.JPEG (JPEG Image, 640x480 pixels) Buckeyball.JPEG (JPEG Image, 640x480 pixels) Mozilla Firefox. Mozilla Firefox. Mozilla Firefox. Assorted Pictures and Movies. Buckeyball movie 12_around_1 (JPEG 26k): Raytrace of 12 transparent spheres closepacked around 1, the template for Fuller's VE (Vector Equilibrium).
Interconnecting sphere centers produces VE. 12_around_1.MOV (Quicktime Movie 109k): raytraced animation of the closepacked sphere cluster spinning. icogeo shows how geodesic sphere is derived from icosa. icosasphere 9 frequency geodesic sphere. Buckeyball.mov (video/quicktime Object) Mozilla Firefox. MISSING NUMBERS. Waterman polyhedra. Waterman polyhedra data generator. Waterman Polyhedra. Waterman Polyhedra. Waterman Polyhedra. Waterman Polyhedra. In the CCP subsets shown here the blue spheres are exactly at the integer multiple radius of sqrt(2 root). Note that some CCP subsets don't have any spheres at that distance, for example, see root 14, 30, and 46.
In these cases the polyhedra are the same as the earlier one, so root 13 is the same as root 14, root 29 is the same as root 30, etc. Waterman polyhedra. Packing spheres If we want to pack identical spheres efficiently we intuitively choose a periodic arrangement like the cubic close packing or CCP. There are three ways to look at this arrangement: the two first are classical and the third has first be highlighted by Steve Waterman. Be patient during the initialization! Different views of the same block show how the layers are arranged.
OGRE – Open Source 3D Graphics Engine. Stella Renders. Stella Users' Polyhedron Models. Here are some models made by people other than me, using measurements or nets generated by Stella4D, Great Stella or Small Stella. If you have made models using Stella, please email me (Stella4D@gmail.com) some images, and I may include them here. Waterman Polyhedra. Play with the controls! Use the "Sequence" slider to step through the series of polyhedra. Click the "Colors" button. If you have red-blue 3D glasses, change the "Stereo Mode" to "Anaglyph".