

Depth-first search. A version of depth-first search was investigated in the 19th century by French mathematician Charles Pierre Trémaux[1] as a strategy for solving mazes.[2][3] Properties[edit] The time and space analysis of DFS differs according to its application area.
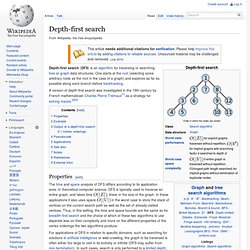
In theoretical computer science, DFS is typically used to traverse an entire graph, and takes time , linear in the size of the graph. In these applications it also uses space in the worst case to store the stack of vertices on the current search path as well as the set of already-visited vertices. For applications of DFS in relation to specific domains, such as searching for solutions in artificial intelligence or web-crawling, the graph to be traversed is often either too large to visit in its entirety or infinite (DFS may suffer from non-termination). Example[edit] For the following graph: Iterative deepening is one technique to avoid this infinite loop and would reach all nodes. Output of a depth-first search[edit] Vertex orderings[edit] Directed Acyclic Word Graph. A directed acyclic word graph stores strings efficiently.

Your DAWG must store thousands of words. It must be faster to use than a regular hashtable, even a highly tuned one with custom hashcodes. Note:This article presents an optimized, special-purpose DAWG structure. A slower, more extensible version is available. Tree Dictionary Benchmark Loading time: 78 ms Program memory used: 17.27 MB Execution time: 1148.2 ms Disk reads: 473 reads Modification: It is easy to modify. Part 5: From Trees to Graphs. Scott Mitchell 4GuysFromRolla.com Update January 2005 Summary: A graph, like a tree, is a collection of nodes and edges, but has no rules dictating the connection among the nodes.

In this fifth part of the article series, we'll learn all about graphs, one of the most versatile data structures.(22 printed pages) Download the DataStructures20.msi sample file. Editor's note This six-part article series originally appeared on MSDN Online starting in November 2003. Note This article assumes the reader is familiar with C#.
Contents Introduction Starting from any node, any other node in the tree can be reached. In Part 3 we focused on binary trees, which are a special form of trees. In this fifth installment of the article series, we're going to examine graphs. Note Realize that all trees are graphs. QuickGraph: A 100% C# graph library with Graphviz Support. There has been a lot of changes to the source code and the article below, since the first submission on Dec. 8.
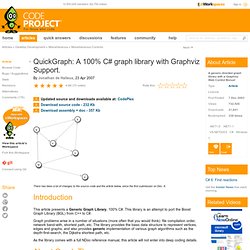
Introduction This article presents a Generic Graph Library, 100% C#. This library is an attempt to port the Boost Graph Library (BGL) from C++ to C#. Graph problems arise in a number of situations (more often that you would think): file compilation order, network band-with, shortest path, etc. The library provides the basic data structure to represent vertices, edges and graphs, and also provides generic implementation of various graph algorithms such as the depth-first-search, the Dijkstra shortest path, etc. As the library comes with a full NDoc reference manual, this article will not enter into deep coding details. About Graph Theory This is a quick remainder about graph theory: A directed graph G=(VxE) consists of a finite set V=V(G) of vertices and a finite multi-set E contained in VxV = {(u,v)| u,v in V} of edges that are ordered pair of vertices.
Graphbook - A book on algorithmic graph theory. A GNU-FDL book on algorithmic graph theory by David Joyner, Minh Van Nguyen, and David Phillips.
This is an introductory book on algorithmic graph theory. Theory and algorithms are illustrated using the Sage open source mathematics software. To get an overview of the book, you can view the table of contents as shown below or download the complete book. This book is more commonly known as the "DaMNeD" book if you notice how our names are used to abbreviate the book. So feel free to call it the DaMNeD book :-) Supplementary materials for the book can be found at A companion book is Explorations in Algebraic Graph Theory with Sage. The book is a work in progress; it is by no means complete yet. The latest revision of the book is called latest-rxxx.