

Géométrie. Courbure terrestre. Objets à grande distance cachés derrière la courbure terrestre La courbure terrestre — nommée aussi dépression — définit l'horizon visuel apporté par la rotondité ou sphéricité de la Terre.
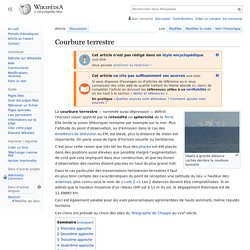
Elle limite la vision (théorique) lointaine par exemple sur la mer. Plus l'altitude du point d'observation, ou d'émission dans le cas des émetteurs de télévision ou FM, est élevé, plus la distance de vision est importante. On parle aussi de ligne d'horizon visuelle ou hertzienne. C'est pour cette raison que très tôt les feux des phares ont été placés dans des positions aussi élevées que possible malgré l'augmentation de coût que cela impliquait dans leur construction, et que les hunes d'observation des navires étaient placées en haut du plus grand mât. La bibliothèque « univers » de Babel. L’idée d’une bibliothèque infinie est imaginée pour la première fois par le mathématicien et écrivain allemand Kurd Lasswitz.
Dans sa nouvelle « La bibliothèque universelle », parue en 1904, soit quelques années avant sa mort, Lasswitz imagine une bibliothèque pouvant contenir toutes les œuvres possibles de l’humanité. Raisonnant en bon mathématicien, il sait que les combinaisons de tous les caractères de l’alphabet aboutissent à un nombre fini. Jorge Luis Borges, écrivain argentin du XXe siècle, s’en inspire et publie en 1941 une de ses plus célèbres nouvelles, « La bibliothèque de Babel ». La bibliothèque de Babel est une bibliothèque univers, c’est-à-dire qu’elle est tellement grande qu’elle contient tous les textes possibles et imaginables, sa taille constitue un défi à l’imagination humaine. Turing, la révolution informatique. Alan Turing est né le 23 juin 1912 et décède le 7 juin 1954.

Malgré la brièveté de son existence, 42 ans, il est un des plus brillants scientifiques du XXe siècle. Il a en effet contribué en moins de 20 ans à plusieurs domaines majeurs : la logique, l’informatique, la biologie, la cryptographie et l’intelligence artificielle. Ses idées ont contribué à former le monde actuel. De Alan à Turing Le père de Turing était un fonctionnaire colonial anglais basé en Inde. À 9 ans, il découvre les sciences grâce au livre Les merveilles de la nature que tout enfant devrait connaître : l’auteur y explique que les êtres vivants fonctionnent comme des machines.Le jeune Turing s’intéresse à la géographie et se met au français pour correspondre avec sa mère à l’insu de son père.
À 19 ans, il est admis à Cambridge, obtient sa licence de mathématiques avec mention, et devient Fellow de King’s College. Turing regardant les marguerites pousser - Croquis de sa mère - © Sherborne School. La théorie du chaos. Tout d'abord la théorie du chaos fut officiellement découverte par Edward Lorenz, professeur de mathématique au MIT en 1961.Mais déjà plus tôt en 1873 James Clerk Maxwell avait fait cette simple observation : «Quand une infime variation dans le temps présent apporte une différence tangible dans l’état d’un système, la condition de ce système est dès lors défini comme étant instable et rend impossible toute prédiction des événements futurs».

De plus on trouve, dans le développement de cette théorie, "l’effet papillon" (voir illustrations) qui représente un systèmes où un événement peut modifier l'ensemble du système de manière inattendue stigmatisé par la célèbre communication d'Edward Lorentz «Est-ce qu'un battement d'ailes de papillon au Brésil peut provoquer une tornade au Texas». La théorie du chaos bouleverse nos conceptions classiques du hasard : il peut exister un ordre dans le désordre de certains phénomènes. Deux des nombreuses représentations de l'effet papillon.
Qu'est-ce qu'un attracteur étrange ? Attracteur de Lorenz Attracteur de Hénon L’attracteur étrange : cette courbe n’est pas celle du mouvement mais représente les états du système et elle montre que dans des cas où on aurait l’impression du désordre, il y a cependant un certain type d’ordre, des lois, d’où l’expression "chaos déterministe".
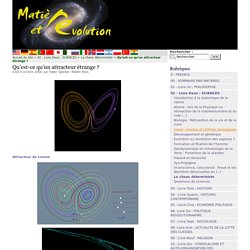
Un attracteur signifie que la dynamique a tendance à être attirée par lui. Par exemple, le fleuve est un attracteur du bassin fluvial. Etrange signifie que la forme de cet attracteur n’est pas une courbe ni une surface et n’est même pas continue mais reconstituée point par point de manière discontinue par la dynamique qui, bien qu’apparemment désordonnée, reconstitue ce type spécial d’ordre. Attracteur de Lorentz du climat. Théorie des jeux - Une idée féconde. Certains liens, certaines associations d'idées et de concepts vont de soi: «recherche» et «université», par exemple, ou «hockey» et «séries éliminatoires».
D'autres toutefois semblent un peu moins «naturelles». Ainsi, qui penserait associer la théorie des jeux à l'économie et aux grands bouleversements qui agitent la société? C'est pourtant ce qu'ont osé faire Oskar Morgenstern et John von Neumann en formulant leur théorie des jeux au milieu des années 1940. Robert Leonard, professeur au Département des sciences économiques de l'UQAM, a voulu éclaircir la naissance de ce concept en publiant un livre sur ce drôle de sujet aux Presses de l'Université de Cambridge. Rejoint au téléphone, il a bien voulu nous expliquer le contexte dans lequel on vient de lui remettre le prix Joseph-J. Le professeur Leonard explique d'abord que l'History of Economics Society décerne un prix chaque année en l'honneur de Joseph J.