

Astrodynamics/N-Body Problem, wikibooks. N-Body Problem[edit] Newton's law of universal gravitation only accounts for two bodies, m1 and m2.
However, in space there are frequently more bodies to be concerned with. We can generalize the problem to say that there is a number N bodies to deal with, and create an equation that can deal with an arbitrary number of bodies. All of the bodies together are known as a system of bodies. When studying the N-body problem, it is important to focus on a single body, whose motion is of primary interest. Where rni is the distance vector between object n and object i. The total force of gravity on the ith object is given as: We also know that the force of gravity on the ith body from the ith body (the force of gravity on itself) must be zero.
Gravitational N-body Problem - Tom's wiki. The gravitational N-body problem is a classical problem in Physics.
Applying our experience in solving Second Order Differential Equations is now an excellent starting point to see how we can integrate Example Python code We use N-body units where G=M=R=1 and make heavy use of pythons numpy package in our example code. In this current implementation it employs a fixed time step and provides some basic plotting for the orbits, energies and some phase space elements. [Expand] Here is a python code which we can use as a laboratory to study problems for a few particles and explore the accuracy of different integration schemes.
N-body choreography, wikipedia. An n-body choreography is a periodic solution to the n-body problem in which all the bodies are equally spread out along a single orbit.[1] The term was originated in 2000 by Chenciner and Montgomery.[1][2][3] n-body choreographies can be discovered using variational methods[1] , and more recently, topological approaches have been used to attempt a classification in the planar case.[4] References[edit] External links[edit]
Euler's three-body problem, wikipedia. In physics and astronomy, Euler's three-body problem is to solve for the motion of a particle that is acted upon by the gravitational field of two other point masses that are fixed in space.
This problem is exactly soluble, and yields an approximate solution for particles moving in the gravitational fields of prolate and oblate spheroids. This problem is named after Leonhard Euler, who discussed it in memoirs published in 1760. Important extensions and analyses were contributed subsequently by Lagrange, Liouville, Laplace, Jacobi, Darboux, Le Verrier, Velde, Hamilton, Poincaré, Birkhoff and E. T. Whittaker, among others.[1] Euler's problem also covers the case when the particle is acted upon by other inverse-square central forces, such as the electrostatic interaction described by Coulomb's law. Two-body problem, wikipedia. In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other.
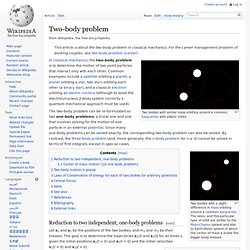
Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other (a binary star), and a classical electron orbiting an atomic nucleus (although to solve the electron/nucleus 2-body system correctly a quantum mechanical approach must be used). N-body simulation, wikipedia. Many-body problem, wikipedia. Examples[edit] Approaches[edit] Quotes[edit] "It would indeed be remarkable if Nature fortified herself against further advances in knowledge behind the analytical difficulties of the many-body problem.
" Further reading[edit] Jenkins, Stephen. Three-body problem, wikipedia. N-body problem, wikipedia. This article is about an ancient, classical problem in classical mechanics.
For the problem in quantum mechanics, see Many-body problem. In physics, the n-body problem is an ancient, classical problem[1] of predicting the individual motions of a group of celestial objects interacting with each other gravitationally. Solving this problem — from the time of the Greeks and on — has been motivated by the desire to understand the motions of the Sun, Moon, planets and the visible stars.
Classical Mechanics.