

Petit panorama du vocabulaire mathématique. En 1966, Jean-Pierre Serre publiait un ouvrage intitulé Algèbres de Lie semi-simples complexes [S-66].

D’après Etienne Ghys, qui a interrogé l’auteur, celui-ci n’avait pas remarqué que son titre était un oxymore … du moins pour le profane ! L’initié sait bien, en effet, que l’adjectif « complexe » ne signifie pas que le sujet soit ardu : il fait référence au corps des nombres complexes. Les Maths, une langue vivante comme une autre?Le Webinet des Curiosités. Les mathématiques sont-elles un « langage » comme on le lit souvent?

La comparaison est tentante, surtout quand on entend à la radio Cédric Villani lire ses formules comme une poésie (à la 19eme minute environ). C’est vrai que le langage mathématiques utilise des symboles et une grammaire bien précise comme n’importe quelle langue. C’est aussi vrai que comme toute langue vivante, sa syntaxe s’enrichit régulièrement de nouveaux concepts et de nouvelles règles. Pour autant peut-on assimiler les maths à une langue comme une autre? Hamilton and the Poetry of Science. I.
Introduction The nature of the relationship between literature and science during the Romantic period is a topic that has provoked lively critical debate for many years now. Numerous studies have sought either to elucidate the many influences that scientific research exerted upon literature, or else to reveal the broader cultural resonances that can be detected within contemporaneous scientific texts, and publications such as Andrew Cunningham and Nicholas Jardine’s Romanticism and the Sciences (1990), Stefano Poggi and Maurizio Bossi’s Romanticism in Science (1994), David Knight’s Science in the Romantic Era (1998), Tim Fulford, Debbie Lee, and Peter Kitson’s Literature, Science and Exploration in the Romantic Era (2004), and Noel Jackson’s Science and Sensation in Romantic Poetry (2008) are only a few of the monographs which explore these sorts of issues.
II. Your Joint Abode William Wordsworth (1770-1850) had first met Hamilton in 1827, and the two men exchanged letters regularly. Maths et extraits de textes littéraires. Poésie fibonaccienne : Fibs. Application poétique des maths. Dans cet article, j’explique une des nombreuses façons dont on peut utiliser des mathématiques en poésie : les mathématiques s’appliquent à la physique, à la biologie ou à la finance (par exemple), mais aussi, même si c’est moins connu, à la littérature.
Commençons donc par un (premier) poème. Le poète est Arnaut Daniel, de l’œuvre duquel il nous reste assez peu de choses ; on sait qu’il a vécu de 1180 (environ) à 1210 (au moins) et qu’il était célèbre et reconnu [1]. Le texte présenté ici est une traduction en français contemporain [2]. On trouvera le texte originel en provençal ici ou là (et même là).
La forme sextine Les six strophes du poème (la dernière, une sorte d’envoi, la tornada, que l’on pourrait aussi bien appeler une coda, n’est pas incluse dans ce compte) sont formées de six vers, les vers de chacune des strophes se terminent par six mots, qui sont les mêmes dans toutes les strophes, mais n’y occupent pas la même place. Intro éducative : Poésie et mathématiques. Michèle Tillard[1] Il n’est pas toujours évident de mettre en lumière des liens pouvant exister entre deux matières que tout semble opposer, en l’occurrence les mathématiques et le français.

Ces liens, pourtant, existent, et c’est ce que j’ai voulu montrer, au lycée Montesquieu du Mans, à deux classes de première fonctionnant en parallèle, et toutes deux bénéficiant d’un effectif réduit de vingt-trois élèves. La séquence s’est étendue sur environ dix-huit heures, réparties sur huit semaines. Un premier cours a consisté à établir les liens, peu évidents, entre les deux matières. En effet, un préjugé tenace veut que la poésie, trop souvent conçue comme pure « effusion lyrique », soit peu compatible avec les chiffres, la rigueur (ou la symbolique) des mathématiques. Poétique mathématique non-probabiliste. Les poèmes mathématiques arabes. Les scientifiques arabes divulguaient leur savoir sous la forme de poèmes qui facilitaient la mémorisation et amusaient en société.
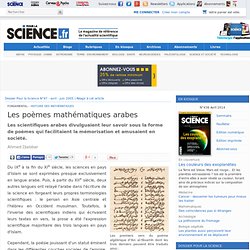
Ahmed Djebbar Les premiers vers du poème algébrique d’Ibn al-Yâsamîn dont les trois derniers peuvent être traduits ainsi :L’algèbre concerne trois choses : le bien, les nombres et la racine.Le bien est tout nombre carré et sa racine est l’un de ces côtés.Et le nombre absolu est ce qui n’est pas rapporté au bien ou à la racine.Comprends cela et tu réussiras. Ahmed Djebbar est professeur à l’Université des sciences et des technologies de Lille. Du ixe à la fin du xie siècle, les sciences en pays d'Islam se sont exprimées presque exclusivement en langue arabe. Puis, à partir du xiie siècle, deux autres langues ont relayé l'arabe dans l'écriture de la science en forgeant leurs propres terminologies scientifiques : le persan en Asie centrale et l'hébreu en Occident musulman.