

Cryptographie et nombres premiers. Youtube. Présentation du Grand oral. L'épreuve orale terminale est l'une des cinq épreuves terminales de l'examen du baccalauréat.
Elle est obligatoire pour tous les candidats qui présentent l'épreuve dans les mêmes conditions. Baccalauréat : comment se passe le Grand oral ? BAC 2021 : INFORMATION IMPORTANTE Pour tenir compte des incertitudes liées à la crise sanitaire, les épreuves de spécialité du baccalauréat général et technologique seront évaluées en contrôle continu.
Les épreuves des 15 au 17 mars sont donc annulées. Les épreuves terminales du mois de juin sont maintenues. Le détail des adaptations de la session 2021 Quel est l’objectif du Grand oral ? Le Grand oral vous forme à prendre la parole en public de façon claire et convaincante. Cette épreuve permet aussi d’utiliser vos connaissances (celles qui sont liées à vos spécialités) pour créer une argumentation et montrer en quoi elles sont essentielles pour votre projet de poursuite d'études, et même votre projet professionnel.
Évaluation du Grand oral L'épreuve est notée sur 20 points. La musique et les mathématiques. Musique et mathématiques. Jedrzejewski Franck, Hétérotopies musicales : modèles mathématiques de la musique.

Hermann, Paris 2019 [670 p.; ISBN 979 1 0370 0067 5 ; 38 €].Nicolas François, Le Monde-Musique. (I), L'œuvre musicale et son écoute. « Musiques xx-xxie siècles », Editions Aedam Musicae, Château-Gontier 2014 [264 p. ; ISBN 978-2-919046-19-5 ; 25 €]Serge Robert, La construction des gammes musicales. Dans « Accromath » 2007.Musique et mathématiques (pour les lycéens).Coulon Rémi, Maths et musique.MAZLIAK LAURENT (Université Paris VI et Quatuor Hypoténuse), Trois millénaires d'une histoire d'amour mouvementée : Musique et MathématiquesSéminaire MaMuX, Mathématiques, musique et relations avec d'autres disciplines.Art, mathématiques, langage et émotion.
Dans « Mathématiques et sciences humaines » (178), École des Hautes Études en Sciences Sociales, été 2007.Séminaire musique et mathématiques, « École » de mathématiques pour musiciens.Mauduit Christian, Pascal Carine, Tomas Nathalie, Musique, maths, physique. La construction des gammes musicales. L’histoire dit que Pythagore s’amusait à faire vibrer des cordes de différentes longueurs et de différentes tensions pour étudier les rapports des sons entre eux.

On peut faire la même expérience sur une guitare. Lorsqu’on fait vibrer une corde de guitare, plus la partie vibrante est longue, plus le son est bas et, vice versa, plus elle est courte, plus le son est aigu. Si on appuie sur une corde à la 12e case, le son entendu sera à l’octave du son de la corde à vide; il aura une fréquence deux fois plus élevée.
Bien entendu, Pythagore ne connaissait pas la physique comme vous; la notion de fréquence lui était inconnue, mais il savait sûrement reconnaître quand un son était à l’octave d’un autre son. Ainsi, deux sons sont à l’octave l’un de l’autre si le rapport de leurs fréquences est égal à deux: On raconte que Pythagore en avait déduit que la hauteur d’un son, qui pour nous correspond à la fréquence f, est inversement proportionnelle à la longueur de la corde: La fréquence. Images des mathématiques. Bernar Venet est un artiste plasticien français, né en 1941 à Château-Arnoux-Saint-Auban dans les Alpes-de-Haute-Provence.

Il réside aux États-Unis où il s’est fait connaître pour ses sculptures d’acier et ses dessins. Site officiel. Vue des peintures murales, 2002 Acrylique sur mur au Ludwig Museum, Coblence, Allemagne, 2002. Les fractales. D'autres images en bas de page Le mot "fractale" vient du latin "fractus" qui signifie "brisé".
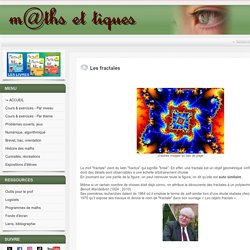
En effet, une fractale est un objet géométrique «infiniment morcelé» dont des détails sont observables à une échelle arbitrairement choisie. En zoomant sur une partie de la figure, on peut retrouver toute la figure, on dit qu’elle est auto similaire. Même si un certain nombre de choses était déjà connu, on attribue la découverte des fractales à un polytechnicien français, Benoît Mandelbrot (1924 ; 2010). De nouvelles perspectives. Les recherches des peintres de la Renaissance en Italie visant à produire des représentations plus réalistes dans les tableaux ont ouvert des perspectives nouvelles aux géomètres.
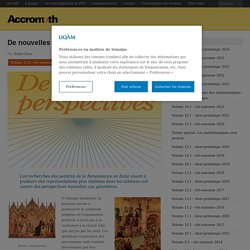
Martini, L’Annonciation Duccio, L’Entrée à Jérusalem. Mathématiques. Les mathématiques dans la vie quotidienne! Images des mathématiques. Pour les États et pour les organisations internationales, comme l’Organisation mondiale de la santé (OMS) ou l’Union européenne (UE), connaître l’évolution d’une épidémie humaine (grippe H1N1, virus Ebola, coronavirus), animale (grippe aviaire, peste porcine, rage) ou végétale est primordial.
En cas de menace sanitaire grave appelant des mesures d’urgence, notamment en cas de menace d’épidémie, le ministre chargé de la santé peut, par arrêté motivé, prescrire dans l’intérêt de la santé publique toute mesure proportionnée aux risques courus et appropriée aux circonstances de temps et de lieu afin de prévenir et de limiter les conséquences des menaces possibles sur la santé de la population.Article L3131-1 du code de santé publique Cette étude permet en effet de prédire l’évolution de la maladie au cours du temps et a pour but principal de guider les dirigeants dans la prise de décision en termes de santé publique.
Le modèle SIR Comment lire ce système ? Solution du modèle SIR. Etienne Pardoux : Modèles mathématiques des épidémies – Briques2math. Etienne Pardoux, Professeur émérite à Aix Marseille Université, nous parle de modélisation mathématique des épidémies.
Les mathématiques détaillées et explications sont dans le texte qui suit ! Introduction Etienne Pardoux : Nous vivons en ce moment une pandémie mondiale inédite. Une addition d’épidémies dans chaque pays, qui se sont répandues par les transports aériens, et qui deviennent des épidémies nationales une fois les frontières verrouillées. Modélisation de mouvement de foule. Cet exposé commence par expliquer les objectifs de la modélisation mathématique de phénomènes complexes à appréhender.

Contrairement à l’étude d’une pierre qui tombe (ou de molécules qui s’entrechoquent), évoqués au début de la vidéo, la situation de personnes cherchant à évacuer une salle ou d’automobiles sur une autoroute est plus complexe à comprendre et ne suit pas un ensemble de règles simples et connues. Un modèle statistique pour la gestion des stocks de poissons. Le maintien de la biodiversité des bancs marins est un enjeu de taille dans un contexte où la demande pour les produits de la mer est toujours en croissance et où la technologie permet de localiser et de capturer cette ressource relativement facilement. Irem.univ-mrs.fr/magistere/grand-oral/